Physical Forces at Work in Bassoon Reeds
By James B. Kopp
James Kopp & Associates
Makers of reeds for the bassoon have a centuries-long head start on acoustical physicists in trying to understand these remarkable little tone generators. Even before the mid- to late 19th century, when modern German- and French-system bassoons were developed, there were earlier bassoons and earlier reed styles for the music of Bach’s and Beethoven’s eras. Still earlier, makers produced reeds for dulcian in the age of Praetorius and reeds for shawm in the age of Henry VIII. The reed maker of today relies to a large extent on slowly evolving traditions: specifications, work habits, and beliefs are handed down from one practical reed maker to another. Various reed designs and production techniques have come to be associated with different types of bassoon (French system versus German system, for example, or modern versus historical), or with narrower national or personal ideals.
Acoustics came later. Scientific explanations of the reed’s working began to appear only in the nineteenth century, and to flourish only in the twentieth century, during the lifetime of the familiar modern bassoon. The physical workings of the bassoon reed are quite sophisticated: a variable air stream and two vibrating blades interact as a system. To make matters more complicated, the tone generator (reed) is coupled to a resonator (the bassoon) that has complicated physics itself, partly because of its conical bore and its finger holes of irregular depth. All these factors have made the bassoon and its reed harder to explain than most other wind instruments. But acousticians have made large strides in the last generation. By the late twentieth century, a respectable scientific literature had grown up on the subject of the bassoon’s acoustics, sometimes including the reed itself.
A survey of the scientific literature, coupled with experience in making reeds for a wide variety of historical and modern bassoons, suggests that the many different types of bassoon reed share certain acoustic fundamentals. Variations of certain physical characteristics – length, width, and thickness of the blades, for example – will have predictable effects in the behavior of bassoon reeds, no matter the type of bassoon or taste of the reed maker. The countless reed styles that exist appear to be different strategies for harnessing the same physical forces.
Bassoon reed makers could learn many useful things from acoustical scientists. Physicists, however, tend to seek quantitative answers to their questions, and only the most mathematically minded of bassoonists have attempted to penetrate the thickets of equations that comprise most acoustical writings. But a middle way is possible: the bassoonist can understand much of the science of the bassoon reed in a merely qualitative way (that is, with no numbers or equations), as long as suitable readings are available. Such a reader will discover a rational basis for many of the traditional beliefs about reed making. Perhaps more important, the bassoonist seeking particular adjustments or improvements in a given reed design will know what steps are most likely to be helpful.
In the following discussion, the emphasis is on physical truths that can be put to immediate practical use by the reed maker, while many topics of more academic interest are neglected. I have avoided much scientific jargon that would be obscure to the average bassoonist, but I have sometimes opted to introduce a useful scientific term rather than engage in a roundabout paraphrase. Many of these terms are italicized, alerting the reader that even a common-looking word has a scientific connotation that may be pursued in a reference book.1 I have numbered and italicized many observations that have immediate practical applications, so that a reader can locate them quickly.
1. Various Models for the Vibrating Bassoon Reed
Much of the following discussion centers on the vibration of the bassoon reed’s blades, and on how the rate of vibration is affected by changes in the reed’s design. This rate of vibration is of pivotal importance to the player, as we shall explain a little later. Meanwhile, there are many useful models for studying the vibrations of the reed. We will mention several before pursuing a few in depth.
The four-phase cycle. The bassoon reed is easier to understand if we begin with an early peek at an overall model of its vibrational cycle. After this, we will go back and examine the constituent parts at a more fundamental level. The double reed of the bassoon vibrates in a cycle of four phases.2 Bassoonists are used to seeing the reed in its first or static phase (fig 1).
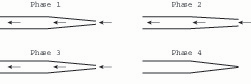
Fig. 1. Four phases in the bassoon reed’s vibrational cycle. Arrows represent air passing through a reed, which is shown in profile. After Campbell and Greated, The Musician’s Guide to Acoustics, 260.
In its second phase, the reed inflates, meaning that the tip aperture increases in area and the corners of the two opposed blades separate slightly from one another. (The reason for this inflation will be discussed below.). By now, suction has been created by the acceleration of the air stream through the reed tube. The suction causes the reed to “deflate”; it passes through a third phase that looks identical to the first phase, and then the tip closes (fourth phase). The pulsation of the air column, aided by the elasticity and tension of the blades, now causes them to spring open again, returning them to the first phase. As long as the player continues the air stream, the cycle will repeat itself, comprising what acousticians call a steady-state oscillation. In the steady state, the reed becomes the slave of the bassoon’s air column, which pulsates in an in-and-out motion. This reciprocal motion is what causes the reed blades to inflate in phase 2: the deflation of phase 4 is reciprocated by an inflation in phase 2.
The system of the double reed is complex in that it combines elements of both solid mechanics (the blades) and fluid mechanics (the air stream). This interaction of the two physical phenomena is a marvel of nature, and a satisfactory linking of the two is the goal of every reed maker, whether the reed maker appreciates this or not. Several physical models are available for studying the movement of the blades and air stream.
One traditional model to be used here is sometimes called the clamped-free elastic bar. A straight bar is firmly clamped in a block heavy enough to immobilize the rod at one end; the other end is free to vibrate (fig. 2).

Fig. 2. First-mode vibration of a clamped-free bar. A straight, elastic bar clamped in a block at one end, free to vibrate at the other end, is shown in the two extreme phases of its vibration.
Being elastic, the rod will recover its shape after deformation (bending). (A very similar model, the cantilevered beam deflection model, has been extensively studied by engineers.) A diving board is a realization of such a model, and so is a clarinet reed.
It’s obvious that the bassoon reed is more complicated in certain ways than a diving board, and only a more sophisticated model will capture more of the subtleties of a real reed’s vibration. Physicists have studied the vibration of plates, which are thinner than bars and have distinct patterns of vibration. Among musical instruments, the cymbal and gong are examples of plates. Plates may also be cantilevered; the airplane wing is an important example. The bassoon reed can be studied as a pair of plates cantilevered (clamped) at one end. The wired tube of the reed is comparable to a clamp, while each blade can be compared to a bar or plate clamped at one end (fig. 3).
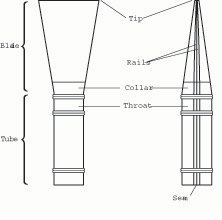
Fig. 3. A schematic drawing of a reed for modern bassoon. Each blade may be compared to a bar clamped at one end. Location of the throat, where the interior cavity of the reed is narrowest, may vary from one reed design to another. The collar (unremoved bark above the first wire) may vary in length or be absent.
Engineers have studied the vibration of even such special cases as cantilevered plates with step-wise variations of thickness, and cantilevered trapezoidal plates. It happens that the blade of a bassoon reed is a trapezoid; its fourth and shortest side is defined by the first wire. (Reed makers and engineers are usually looking at vibrations through opposite ends of the same telescope. Engineers usually seek to minimize vibrations, so they generally cantilever their trapezoidal plates on a long side. Reed makers, in contrast, seek maximum vibration [within limits], so the trapezoidal blades of the reed are always connected to the tube on the shortest side.)
Yet even these special cases do not take account of the internal cavity between the paired blades. Each blade may also be considered as a shell, which is a special category of plate, marked by both concavity and convexity. A bell is a musical example of a vibrating shell. Engineers have studied the vibrations of certain types of shells, and the analysis has proved to be extremely complex. Scientists have also studied the vibrations of membranes, which differ from simple plates in being held under tension. A drumhead is a musical example of a vibrating membrane. The bassoon reed also has certain tensions applied to it, by the wires and binding that deform the cane from its original circumference.
A further complication is that arundo donax, the cane from which bassoon reeds are made, is a discontinuous material having several interesting characteristics that affect its vibration. It is layered (containing both “bark” and pith) and its barky outer layer is more elastic (stiffer) than the pithier inner layer.3 Moreover, the cane has multiple dimensions of elasticity that affect the reed’s vibration. Two of these will concern us here: the longitudinal (lengthwise) and the circumferential (along the curve of the bark).4
The vibration of a bassoon reed is an example of forced vibration, meaning that a force has been continuously applied to the surface, sustaining the vibration. The force here is not, physically speaking, the air stream supplied by the player, but rather the oscillations of the air column in the bassoon. It is true, however, that the air stream -- beginning in the player’s body, continuing between the blades, and passing through the crook into the bassoon – is the energy source for these oscillations.
Specialists in the field of fluid mechanics study the flow of air and other fluids, including the suction effect that helps close the bassoon reed in its fourth cycle. One researcher has suggested that two very complex models from the field – vortex shedding and flapping flutter – may eventually be found to be applicable to the study of bassoon reed vibration.5
While all these models have particular virtues, the clamped-free bar appeals most directly to the intuition of the non-physicist. It is also a model whose operations can be directly translated into principles of general use by reed makers. While use of the model is illustrative and thought provoking, we must remember that it gives only a crude approximation of a few aspects of a reed’s behavior; many complications and subtleties are purposely ignored here. Before we turn to this model, however, we must understand a little more about the role the reed plays in the acoustic system of the bassoon.
2. The Reed as Part of the Acoustic System of the Bassoon
The proper size of a bassoon reed is mandated by the truncation of the bassoon’s air column. The air column (bore) is a long, gradual cone, except that a portion of the small end is missing (fig. 4).

Fig. 4. A schematic drawing of the air column of the bassoon. The apical portion is not literally present, its place being taken by the reed.
The maximum diameter at the bell is about 40 mm. The smallest diameter actually present, at the small end of the bocal, is about 4 mm. If the cone’s taper continued beyond the bocal tip to the theoretical end of the cone, the “missing” portion of the cone would be almost a foot long. To be an effective tone generator, the reed must take the place of this missing apical portion (named after the apex or tip). The static size of the bassoon’s reed measures less than one-quarter of this missing length.
Acousticians use the term equivalent volume to describe how much of the missing apical portion a given reed serves to replace; a good reed replaces 100% of the missing volume. But the missing volume is not a simple matter of the reed’s internal volume. Instead, equivalent volume is measured in terms of vibrational size, which is always larger than the static size. Because any functioning reed’s blades are flexible, they effectively increase the size of the reed. The flexibility of the blades is associated with a physical quality called compliance.6 Many reed makers understand compliance intuitively, even if they do not use the term. Increased compliance lowers the frequency of a vibrating body; in the bassoon reed, it makes for an easy crow and easy low-note response, among many other effects.7 Lower compliance raises the frequency of a vibrating body; in the bassoon reed, it makes for a reluctant crow and easy high-note response. In achieving a perfect vibrational size for a bassoon reed, the maker must balance the reed’s static size with a suitable amount of compliance.
I’ve promised the reader an equation-free article, but I’m going to make a brief and painless exception here. The following equation simply restates the gist of the preceding paragraph:
Vibrational size of a reed = Static size + Compliance
If we wish to isolate (and thus define, in a non-scientific way) the compliance of a bassoon reed, we can instead say:
Compliance = Vibrational size – Static size
Calculating the actual quantity of this compliance would be quite a chore even for a trained physicist, and the numerical answer would be of little use to the average reed maker. (Physicists express compliance in terms of displacement per unit of force, or meters per newton.) But we can say that a successful bassoon reed has enough compliance for easy low notes, but not so much that high-note response becomes difficult. In the following discussion, we will point out which design factors increase compliance in the reed, and which factors decrease compliance.8 Without troubling to calculate the meters per newton of compliance in our reeds, we can benefit from understanding the underlying tendencies. It’s useful to remember, during the following discussion of the reed’s vibration, that frequency and compliance are inversely related.
3. Vibration of a One-Dimensional Reed: The Clamped-Free Bar
The interplay of two physical qualities, mass and elasticity, gives rise to vibrations in mechanical systems, including the bassoon reed.9 As used in this study, elasticity denotes resilience or stiffness – the tendency for a material to return to its original shape after being deformed. Physicists have studied the transverse vibrations of a rod or bar that is firmly clamped at one end and free at the other. This is called a clamped-free bar, and a similar vibrating reed is called a clamped-free reed. The frequency at which such a bar vibrates may be controlled in predictable ways by modifications to the shape and length of the bar. Rises in frequency are associated with reduced compliance; drops in frequency are associated with increased compliance.
The frequency of the vibrating bar may be lowered by lengthening the bar or by uniformly reducing the thickness of the bar. The frequency may be raised, conversely, by shortening the bar, or by uniformly increasing the thickness of the bar (figs. 5a – 5e).

Fig. 5a. A clamped-free bar of a given length and thickness vibrates at a given frequency. The following comparisons refer to this given frequency.
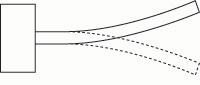
Fig. 5b. If the bar is lengthened, the frequency drops.
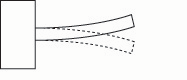
Fig. 5c. If the bar is shortened, the frequency rises.
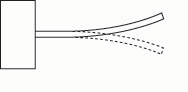
Fig. 5d. If the bar is made thinner overall, the frequency drops.
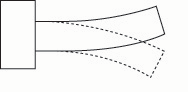
Fig. 5e. If the bar is made thicker overall, the frequency rises.
In influencing frequency, length is much more important than thickness.10
The frequency of the vibrating bar may also be lowered by loading the end; for example, a weight could be soldered or glued onto the free end of the bar. It is not a casual matter to calculate the exact frequency drop caused by loading the bar, but it is generally true that the closer to the free end such a weight is added, the greater the frequency drop; the greater the weight added, the greater the frequency drop. The matters of length, thickness and loading can be directly compared to characteristics of a bassoon reed’s blades; within limits, the blades can be long or short, thick or thin, and of a greater or lesser slope. Here we will mention only the effect of variation in the first dimension (length).
1. A longer blade will be more compliant, if other factors remain constant; a shorter blade will be less compliant.
It is also worth noting that these characteristics are most consistent when the clamped end of the vibrating bar is completely immobilized by a clamp of sufficient mass. The reed’s tube and binding add some stability and mass, but the adjustable wires represent a complicating factor, which is discussed later.
4. Vibration of a Two-Dimensional Reed: The Flared Blades
The frequency of a clamped-free bar may be lowered by loading the free end (adding mass) (fig. 6a).

Fig. 6a. If the bar is loaded at the free end, the frequency drops.
Thus the flare of a bassoon reed’s blade has the effect of increasing the reed’s compliance, because it adds width (mass) to the free end (figs. 6b – 6d).

Fig. 6b. A bassoon reed’s blade may be compared to a clamped-free bar. The following comparisons refer to a blade of a given size, as shown here.
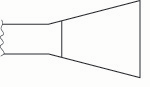
Fig. 6c. If the tip is made wider, the frequency drops.
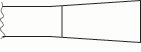
Fig. 6d. If the tip is made narrower, the frequency rises.
2. The broader the tip for a given tube, the more compliant the reed.
3. Conversely, narrowing the reed’s tip, given a constant tube diameter, lessens the reed’s compliance.
Another means of lowering the frequency of a bar is by reducing the cross section (subtracting mass) near the clamped end. This is analogous to narrowing the back of the reed’s blade (figs. 7a – 7b).
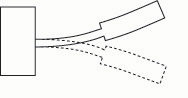
Fig. 7a. If a clamped-free bar is made narrower near the clamped end, the frequency drops.
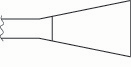
Fig. 7b. If the back of bassoon reed’s blade is made narrower, the frequency drops.
4. The narrower the tube for a given tip width, the more compliant the reed.
The reverse is also true: increasing the cross section near the tube end will raise the frequency. This is analogous to widening the back of the reed’s blade (fig. 7c).
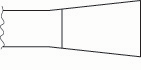
Fig. 7c. If the back of a bassoon reed’s blade is made wider, the frequency rises.
(In practice, widening the back of the blade will also increase the tube diameter, which will increase the reed’s static size.)
5. Increasing the tube size, as long as the tip width remains constant, lowers the reed’s compliance.
We may say all this a little more concisely by referring to the ratio of tip width to throat width11 (figs. 8a – 8c).
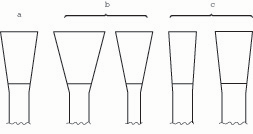
Fig. 8a. A bassoon reed of a given size has a given tip-to-tube ratio. Fig. 8b. In comparison, these two reeds have a greater tip-to-tube ratio. Fig. 8c. In comparison, these two reeds have a smaller tip-to-tube ratio.
6. The greater the ratio of tip width to throat width, the greater the compliance; the smaller the ratio, the lower the compliance.
The reed will vibrate only within a fairly narrow range of tip-to-throat ratios.
If the reed’s blades are curved in the second dimension (which a bassoonist would call the shape), the curve will have predictable but mixed effects on the reed’s internal volume, and thus on its static size. Suppose, for the purposes of discussion, that we have a reed of a given design, including straight rails, in which static size and compliance are in perfect balance. Changing the rails of this reed to convex (only a theoretical possibility for the given reed, of course) would result in increased internal volume. Given our introductory equation, this would demand that some compliance be subtracted by means of some other design factor, so that the reed does not become overly compliant, with difficult high-register response (figs. 9a – 9b).

Fig. 9a. A given bassoon reed with straight rails has a tip aperture with a slight compound curve.
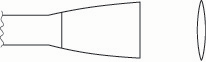
Fig. 9b. A bassoon reed with convex rails has a more elliptical aperture.
(Convex rails lead at the same time to decreased damping of the reed tip aperture, another significant effect. Damping refers to the tendency of vibrations to diminish and die. Here we use the term tip damping or corner damping to denote the pressure of the opposed blades at the corners, which causes the tip aperture to assume a compound curve.)
If the rails on the given straight-sided reed are made concave, the resulting reed will have less internal volume. This will dictate that more compliance be added elsewhere in the reed design, if a proper total vibrational size is to be maintained. (The concave rails also result in more damping of the tip [fig. 9c].)

Fig. 9c. A bassoon reed with concave rails has a more severe compound curve at the aperture.
The collar of the bassoon reed (the bark that extends above the first wire) may in one sense be considered part of the block that immobilizes one end of the vibrating blade. But the collar is not massive enough to remain immobile itself, so this effect is mitigated. The collar plays other roles, however. (We cannot add a collar to an existing reed that lacks one, but let us speak theoretically of doing so.) Adding mass to the back end of a given reed (that is, converting part of its scraped blade into an unscraped collar) has at least two countervailing effects. It (a) increases cross-section near the clamped end, which lessens the compliance of the blades. It also (b) increases tension on the tip aperture, making it rounder and more open. This increases internal volume, which helps to offset the reduced compliance described in (a).
5. Vibration of a Three-Dimensional Reed: Effects of Profile, Forming and Scrape
The third dimension of our reed model is that of thickness. Whereas the blade of a bassoon reed widens towards the tip in the second dimension, it narrows towards the tip in the third dimension. This latter thinning towards the tip is essential in allowing a suction that completes the oscillation cycle of the bassoon reed. Fairly thick tips are not unknown, but they often require a thicker gouge (which places a softer, pithier stratum of cane at the tip) or softer cane altogether, or some other mitigating factor. The necessary balance of stiffness and flexibility (that is, a suitable compliance) in the blades imposes operating limits in the third dimension of the reed, especially in the 1 to 2 mm closest to the tip.
We can again make useful predictions from the clamped-free bar model.
7. A thicker front or thinner back, within limits, tends to increase the reed’s compliance (figs. 10a – 10c).
![]()
Fig. 10a. A bassoon reed’s blade, seen in profile, has a front (right) and back of given thicknesses, and a given oscillation frequency.
![]()
Fig. 10b. If the front of the blade is made thicker, the frequency drops.
![]()
Fig. 10c. If the back of the blade is made thinner, the frequency drops.
8. A thinner front or thicker back, within limits, tends to lower the reed’s compliance (figs. 11a – 11c).
![]()
Fig. 11a. A bassoon reed’s blade, seen in profile, has a front (right) and back of given thicknesses, and a given oscillation frequency.
![]()
Fig. 11b. If the front of the blade is made thinner, the frequency rises.
![]()
Fig. 11c. If the back of the blade is made thicker, the frequency rises.
Above we discussed the basic effects of the shape of a reed’s blades (that is, width, or the second dimension). But these were confined to an ideal or theoretical realm. In practice, a two-dimensional piece of gouged and shaped cane, upon being profiled, formed and scraped by the reed maker, undergoes certain deformations of its second dimension (width). These deformations of the width by introduction of the third dimension are relatively minor, but they are predictable, and worth enumerating here.
The blades of the reed. The two-dimensional blade shape is deformed during the forming process, the basic principle being that the two-dimensional flare becomes exaggerated. The tip shrinks least, while further from the tip, the shape loses more and more of its two-dimensional width. A straight-sided blade remains straight, but assumes a greater angle from the tube than before forming. A concave side becomes mores concave. A convex side becomes less convex.
The tube. The tube portion of the reed undergoes a straightforward transformation during the forming process from rectangle to semi-cylinder. A tube that measures 8.5 mm at the throat when flat will measure less after forming, perhaps 6 x 7.5 mm. The actual diminution of formed width depends on several factors: cane hardness, gouge thickness, use of overlapping versus square seams, the mandrel taper and depth of insertion, the tautness of wires upon forming, and the presence or absence of bevels in the tube.
The point in the air stream at which the reed’s internal cavity reaches its minimum diameter is called the throat. This often is located where the reed tube begins, under the first wire, but it may be lower. A throat below the first wire will decrease the reed’s equivalent volume and increase suction in the fourth phase of the vibration cycle. It will also tend to lessen the leverage of the second wire. (These secondary effects are discussed below.) Beveled edges on various parts of the tube seams have the same effect as analogous reductions in width of the two-dimensional shape. For the reed maker, however, the difference is a practical matter, as a pre-narrowed shaper may not be available.
Depth of the blade cavity. A thinner profile or contour before forming will decrease the internal volume of the formed blank and finished reed, as one reed maker pointed out.12 This is because thinner blades take on a compound curvature, when viewed in cross section (figs. 12a – 12b).
![]()
Fig. 12a. Elliptical tip aperture of a reed blank formed using a thick profile.
![]()
Figure 12b. Compound curve of the tip aperture of a reed blank formed using a thin profile.
Even if scraped to a similar thickness, a thicker-profile reed will have less of this compound curve. Later wire adjustments cannot completely erase the different strains that contrasting profiles may introduce upon forming of the blank. As a general principle, thinning the blades (by scraping, filing, or sanding) tends to increase compliance of the reed. But in practice, thinning often goes hand in hand with wire adjustments, making the question of resulting compliance changes very complex.
Wires and leverage. Early bassoon reeds, which had a relatively small tip-to-throat ratio, were often made without fully adjustable wires. Sometimes only inflexible metal rings were present. But as a reed’s tip-to-throat ratio grows larger, wires become increasingly necessary to open the tip to a functional aperture. An average reed for modern bassoon, after forming, has a tip-to-throat ratio of about 2/1. An oboe reed, by contrast, has a tip-to-throat ratio of about 7/5. The modern oboe staple is oval in cross section, which helps maintain the desired tip aperture.
The presence and adjustment of two wires near the top of the reed tube creates special conditions in the clamping and constraint of the blades. In one sense, the shape of the wires affects the geometry of the blades, which is part of the thickness or radial dimension under discussion here. But in practice, the geometry of the tube, wires, and blades is closely bound up with the tension applied to the tip aperture. Accordingly, we will take up discussion of the wire and tube shape in our later consideration of tip tension, a fourth dimension.
6. The Air Stream of the Bassoon Reed
The transient states. The vibration cycle described in our introduction to the four-phase cycle of the bassoon reed is called the steady state oscillation. But the reed does not proceed immediately from silence to the steady state. In the same way that instruments (including the bassoon) pass through an initial transient and a decay transient, the reed passes through transients going to and from the steady state. During the initial transient, the reed makes the transition from its own oscillation frequency (the crow) to a regime of oscillation with the bassoon’s air column, in which the reed becomes “enslaved” by the air column. Physicists know relatively little about the transient states of the bassoon reed, but they know that they are important in giving the bassoon its characteristic tone.13 During the initial transient, the phase 2 inflation of the reed blades is probably due to increased air pressure from the player’s air stream, but this is not true once the steady state of oscillation begins.
The steady state. In its first or static phase, the bassoon reed is at what a physicist would call atmospheric pressure. When we begin to blow air into a reed (during the initial transient), we raise the air pressure, causing the blades to “inflate,” or open further (second phase). Air begins to pass through the reed tube. Because the tube is narrower than the blades, the air accelerates, just as water forced through a hose nozzle accelerates. The upstream pressure, supplied by the player’s abdominal muscles, is above atmospheric, a physicist would say.
This is an instance of a Bernoulli effect, a physical force arising from a sudden narrowing of the air column: as an air column narrows, the downstream pressure decreases, and the result of this is that the air speed increases. The acceleration of air through the reed tube creates a suction (or negative pressure), which causes the blades to “deflate,” passing through the static position (third phase), until the tip closes (fourth phase) (fig. 1).

Fig. 1. Four phases in the bassoon reed’s vibrational cycle. Arrows represent air passing through a reed, which is shown in profile. After Campbell and Greated, The Musician’s Guide to Acoustics, 260.
Note that this suction-induced fourth phase is affected by the geometry of the internal cavity between the reed’s blades. The cross section of the internal cavity (when the reed is inflated, second position) steadily decreases in area as one moves from the tip toward the throat, owing to both the flare (or tip-to-tube ratio) and the second-phase opening of the reed’s blades. These contribute to the Bernoulli effect, which leads to the acceleration, and thus to the fourth-phase closing of the reed tip.
We have arrived now at the interplay of the air stream and the vibrating blades, and thus at the interaction of fluid and mechanical forces in the bassoon reed. The player’s blowing and the consequent suction-induced rebound are fluid forces, but tension and elasticity – mechanical forces – are critical in allowing the reed blades to return to the static position from phases 2 and 4. For the reed to “inflate” and “deflate” properly (i.e., to move satisfactorily from phase 1 to 2 and from phase 3 to 4, in both cases away from the static position) the reed must be sufficiently flexible, or compliant. For the reed to return to the static position (i.e., to move from phase 2 to 3 and from phase 4 to 1), it must be sufficiently stiff, or elastic.
The proper management of various types of Bernoulli-induced suction is a matter of concern to the bassoonist and reed maker.14 We can enumerate some of the practical aspects as follows.
9. The narrower and/or longer the reed tube, the faster the air stream, other factors remaining unchanged.
10. The wider and/or shorter the reed tube, the slower the air stream, other factors remaining unchanged
Note that great air speed is not a virtue in itself; the virtue lies instead in the right amount of suction to keep the cycle going smoothly, rather like the timing on a car engine. Use of a throat reamer or increased reaming of the butt increases the internal diameter. A reed with an overly narrow throat, or an overly long throat, may create too much suction, so that the reed stays deflated too easily. In other words, the reed can “close down” and refuse to continue vibrating, especially if blown hard. Conversely, an overly wide or overly short throat can make the reed feel reluctant to vibrate, because too little suction is generated to continue the cycle smoothly.
The effect of the reed tube’s dimensions upon Bernoulli-induced suction is more important than their effect on tuning; changes in the suction probably contribute to any timbral difference that bassoonists perceive as being related to tube dimensions.
Turbulence. Blunt (square) edges and rough surfaces in an air column are likely to give rise to turbulence, consisting of tiny eddies or vortices. Turbulence interferes with the streamline flow of the air column, leading to white noise and possibly to erratic cycling of the reed.15 Streamlining the reed tip helps minimize turbulence. Sudden constrictions in the air column also tend to create turbulence. Protruding cane fibers in the tube are one possible source of such a constriction; a crimped or overly thick bocal tip is another.
7. A Fourth Dimension of Reed Vibration: The Effect of Tip Tension
The tip aperture of the bassoon reed is under tension, giving it some of the qualities of a vibrating membrane. The tensional force results primarily from the deformation of the cane’s original circumference into a flatter ellipse (the tip aperture). We will call this force tip tension, since it manifests itself at the reed’s tip aperture. It is distinct from elasticity in the three familiar dimensions we discussed above. Tip tension is present even in unwired double reeds, such as oboe reeds; differing ratios of circumference to tip width will yield different degrees of tension in the tip aperture. A secondary source of tip tension is the reed tube, a tighter ellipse into which the circumference is forced. Deformation of the tube by means of the upper two wires, as discussed below, affects the tip aperture in predictable ways.
The curved gouge. The particular size of cane tube chosen for bassoon cane is a reasonable compromise between the flatter arc of the reed tip and the rounder tube of finished reed, which is warped to a tiny arc by the forming process (figs. 13a – 13c).
![]()
Fig. 13a. The natural arc of a piece of bassoon cane before forming.
![]()
Fig. 13b. The flattened arc at the tip aperture of the same piece of cane, shown after the reed blank is formed and opened. Dotted lines show the original arc.
![]()
Fig. 13c. The tighter arc of the tube portion of a formed bassoon reed blank, shown at the first wire. Dotted lines show the original arc.
Bassoon cane tubes typically measure 22-24 mm in outside diameter. When split, they retain this arc. When the cane is gouged, however, the arc becomes flexible. If soaked for several days and allowed to dry untouched, the cane often cups to a smaller arc, especially if gouged very thin. The profiling process seems to lessen the cupping force, confirming that the bark is the source of this cupping or tension. Most reed makers favor an elliptical gouge, which tends to exaggerate the rounding of the tip aperture, since the corners are of harder cane.
The tip aperture. It is noteworthy that makers of oboe reeds, who often use no adjustment wires, regularly choose from a variety of cane diameters, with the goal of controlling the shape of the tip aperture. One supplier, for example, offers to sort oboe tubes in .50 mm increments, from 9.5-11.25 mm. The smaller the original cane circumference, the greater its deformation after forming the reed, and the greater the tension applied to the tip.
11. The smaller the cane diameter, the more open the tip aperture, all other design factors remaining constant.
The more bark present in a reed blade, the stronger the effect of tip tension upon the tip aperture. The presence of a collar above the first wire, as discussed above, also helps open the tip aperture. When reeds are made in a historical style (with a short scrape and, often, a graduated gouge), the bark portion of the blade is long enough to maintain the tip aperture, even in the absence of a heart in the scraped portion.
Wire adjustments and placement. For purposes of discussion, let us assume that a reed has a round tube wound in a perfectly circular ligature of snugly fitting wires, and blades thin and moistened enough to be suitable for vibration and music-making. Deformation of the first wire will have a direct effect on the tip aperture.
12. Compressing the first wire from top and bottom (making it a horizontal oval) tends to close the tip aperture (figs. 14a –14b).
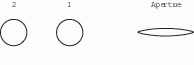
Fig. 14a. Schematic representation of the effects of wire deformation on the reed’s tip aperture. In this “neutral” adjustment, wire 2 is round, wire 1 is round, and the tip aperture is a medium ellipse.
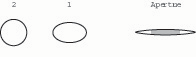
Fig. 14b. When wire 1 is deformed into a horizontal oval, the tip aperture closes, especially in the axial portion (shaded).
13. Compressing the first wire from the sides (making it a vertical oval) tends to open the tip aperture further, especially in the center of the tip (fig. 15).
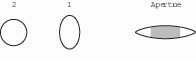
Fig. 15. When wire 1 is deformed into a vertical oval, the tip aperture opens, especially in the axial portion (shaded).
Because the first wire is axial with the center of the blade’s tip, deformations of it from the circular tend to have the greatest effect on the center of the aperture.
By virtue of its position closest to the blades, the first wire also acts as a fulcrum, inverting the respective actions of the second wire. Control of the tip aperture via this fulcrum by deformation of the second wire is occasionally referred to in this discussion as leverage. Bassoonists commonly refer to deformations of the wires as adjustments, and so shall we.
14. Compressing the second wire from top and bottom (making it a horizontal oval) tends to open the tip aperture further (fig. 16).
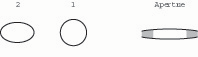
Fig. 16. When wire 2 is deformed into a horizontal oval, the tip aperture opens, especially in the off-axial portions (shaded).
15. Compressing the second wire from the sides (making it a vertical oval) tends to close the tip aperture (fig. 17).
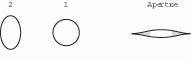
Fig. 17. When wire 2 is deformed into a vertical oval, the tip aperture closes, especially in the off-axial portions (shaded).
The effects of the second wire deformation are transmitted from beyond the first wire, so they tend to have a secondary effect on the tip. As long as the first wire continues to influence the axial portion (the center) of the tip aperture, deformation of the second wire is most noticeable in the off-axis portions of the tip (the corners). In practice, the two wires are adjusted in tandem, by trial and error, until the desired aperture is obtained.
The wire adjustment and leverage model is limited in an important sense by the mutual constraint of the opposed blades. The opposed corners of the two blades touch or nearly touch when the reed is in the static position (depending on the design and the wire adjustments). This touching obviously limits the movement of each blade, causing vibration to end quickly after each cycle. In other words, this built-in constraint is a major source of damping. The opposed corners separate in phase 2, when the reed is “inflated,” but are touching or nearly so in the other three phases. This structural damping of the reed design is always present, but wire adjustments allow the player to increase or decrease it to some extent.
There must be enough separation between wires 1 and 2 for the wire leverage to take effect. But if there is too much separation between these two wires, the cane will not transmit the rounding or flattening, especially if the cane is soft. Harder cane will transmit wire leverage further than softer cane, in both blade and tube. Increased slackness of the two wires will diminish or even nullify the effect of wire deformations.
8. The Embouchure’s Effect on Vibration
So far we have largely been discussing generation, or the positive aspect of vibration. We have briefly referred to damping, which is the stifling of vibration. A bassoon’s reed is always damped in the sense that the constraint imposed by the two opposed blades limits their travel or vibration. A reed may be further damped by other design factors or by wire adjustments, as we have noted. It may also be damped by action of the player’s lip pressure, jaw pressure, and oral cavity.
Acousticians have frequently lumped the last three together under the heading of lip damping. These techniques have the important function of singling out a particular resonance peak, while suppressing other ones. It is interesting to note that the bassoon, unlike the clarinet, can be played, in a very crude way, without any reliance on lip damping. Gripping the reed with the lips “too far onto the reed,” between wire 1 and wire 2, the player can produce the entire first register (BB-flat to f), albeit with a raw tone quality and little control of volume. But a command of lip damping techniques (in other words, a well-developed embouchure) is essential for artistic playing. By this means the bassoonist is able to achieve maximum resonance for a given pitch; this is partly because the lips themselves begin to vibrate along with the reed.16 Lip damping is also important in allowing the player to stabilize the pitch level during changes in dynamics.
Before the adoption of the whisper vent (late 18th to early 20th century), the middle register of the bassoon had virtually identical fingerings to the lower register; only by a change in lip damping was the first or second octave chosen. A skilled use of lip damping techniques helps the bassoonist avoid squawks or cracked notes, which are unwanted response modes, often an octave higher or lower than the intended pitch. The closer the lips are to the tip of the blades, the greater the damping, because the travel of the blades is at a maximum at the tip.
Some bassoonists intuitively shape the oral cavity to improve timbre and tuning. Some others have developed a system of “vowel visualization” techniques, shaping the vocal cavity as they would in speaking or singing a variety of vowel sounds.
The bassoonist may also use jaw pressure to close the reed tip aperture to a greater or lesser extent. Partly closing the reed tip aperture through lip pressure (or biting) has the effect of reducing the internal volume of the reed. Conversely, lowering the jaw will allow the aperture to reach maximum size, increasing the internal volume.17
The clamped-free bar model has allowed us to relate many characteristics of the vibrating bassoon reed to a set of well-understood physical principles. There is no need to repeat here the many characteristics of reed design noted in italics during the preceding discussion. But we may stress again that certain design choices increase the reed’s compliance; certain obverse choices lower the compliance. A proper vibrational size – resulting from a complementary relationship of compliance and static size – is essential to the proper functioning of a bassoon reed. In the simplest of terms, lower compliance makes for good high-register response and a resistant crow, while the higher compliance makes for good low-register response and an easy crow. Most of these design choices are fairly simple to understand in isolation, but their mutual interactions in a vibrating reed can be very complex. The successful combination of design choices is both the métier of the reed maker and a fitting area of future study by acoustic physicists.
The reed maker checks the size, shape, and resistance of the tip aperture first in attempting to finish or adjust a reed that is not quite satisfactory. From our discussion, it is clear that the tip aperture is also of fundamental importance in the reed’s physics. The aperture must be flexible enough to depart from its static position, inflating in the second phase and deflating in the fourth phase of the vibrational cycle. Yet is must have enough restoring force (elasticity) to return to the static position in the first and third phases.
The aperture of the static tip is controlled by the tip-to-throat ratio, the finished blade length, and the scrape of the tip, and also by the placement, tautness, and deformation of the adjustment wires. Additional forces control the movement of the vibrating reed tip: elasticity (a force of the third or radial dimension of the cane), tip tension (derived from the fourth or circumferential dimension of the cane), and the suction resulting from the narrowing of the air stream.
In a well-adjusted reed, third- and fourth-dimensional forces – elasticity and tension, respectively – will be present in a complementary relationship. The stiffer the cane present in a reed – whether through cane selection, gouge thickness, gouge radius, collar length, thickness of scrape – the stronger the fourth-dimensional force (tension) will be, and the less need for wire adjustment. Conversely, the less elastic the cane present, in the respects enumerated above, the weaker will be the effect of tension upon the tip aperture, and the greater the need for wire adjustment. Soft cane may yield a smaller throat, resulting in increased suction and a stronger force toward deflation (fourth phase).
All these physical forces, which work together to establish the reed’s vibration, may be actively managed in the design of reeds of widely varied characteristics, suitable to the individual needs of players. The bassoonist who understands this will have a valuable advantage in producing and improving the reeds that bring his or her instrument to musical life.
Copyright 2003 by James B. Kopp
I am grateful to two colleagues who read this article in draft and made numerous useful suggestions. Donald J. Casodante, who wrote a dissertation about the clarinet reed, was a rich source of insights about the state of research in reed physics and botany. Frank A. Morelli, the well-known performer and teacher, ably represented the bassoonist’s point of view.
1. See, for example,
John Backus, The Acoustical Foundations of Music, second ed. (New York:
Norton, 1977); The McGraw–Hill Encyclopedia of Science & Technology,
8th ed. (New York, 1997).
2. Murray Campbell and Clive Greated,
The Musician’s Guide to Acoustics (London: Dent, 1987), 260.
3. Botanically speaking, only trees
can have bark; the outer layer of Arundo donax is properly called the
epidermis or sclerenchyma. Bassoonists virtually never use either of these
terms, however; they almost invariably call the outer layer “bark.”
In deference to these readers, I will follow the customary (if unscientific)
usage here.
4. Strictly speaking, the cane of
the bassoon reed, Arundo donax, is a viscoelastic material, having qualities
of both a fluid and a solid. For a detailed explanation, see Donald J.
Casadonte, “The Clarinet Reed: An Introduction to its Biology, Chemistry,
and Physics” (D.M.A. diss: The Ohio State University, 1995), 279-83.
In this article, however, we will be focusing on the elastic characteristics
of its solid aspect.
5. Casadonte, “The Clarinet
Reed”, 344; Donald J. Casadonte, personal communication, March 2003.
6. Cornelis Johannes Nederveen, Acoustical
Aspects of Woodwind Instruments, revised ed. (DeKalb, Illinois: Northern
Illinois University Press, 1998), 5, likened compliance to the elongation
of a spring (in an analogous model of vibration). He pointed out that
in the case of a bar clamped at one end, “compliance and mass …
are distributed along the whole vibrating system.” This is also
true of the vibrating blade of the bassoon reed.
7. “In reed-blown instruments
the reed properties, such as size, shape, compliance and damping, are
essential for proper tuning. The reed compliance causes a lowering of
the frequency. In conical instruments, the reed compliance has the same
effect as a [clarinet] mouthpiece cavity, and therefore, it has an important
function in keeping the upper register in tune with the lower one.”
Nederveen, Acoustical Aspects, 97.
8. Bassoonists often use the term
“free-blowing” to describe a reed that is very compliant,
and “resistant” to describe a reed that is less compliant.
I have avoided use of the term resistance in this paper, because its specific
physical meaning is not an antonym for compliance. Moreover, bassoonists
commonly use the single term resistance to describe effects due variously
to damping and to blade stiffness. To the player, these may seem related,
but to the physicist, they are quite separate.
9. McGraw-Hill Encyclopedia of Science
and Technology, s.v. “Vibration.”
10. “The frequency of a [tuning]
fork will therefore directly as the thickness of the prongs … and
inversely as the square of the length of the prongs.” Encyclopedia
Britannica (1949 ed.), s.v. “Vibration.”
11. For a discussion of this topic,
see David Hogan Smith, Reed Design for Early Woodwinds (Bloomington and
Indianapolis: Indiana University Press, 1992), 15.
12. Mark G. Eubanks, Advanced Reed
Design & Testing Procedure for Bassoon (Portland, Oregon: Arundo Research
Co., 1986, 2.
13. See John Backus, The Acoustical
Foundations of Music, second ed.(New York:Norton, 1977), 118, for further
details.
14. Arthur H. Benade, Horns, Strings
& Harmony (Garden City, New York: Anchor Books, 1960), 161-63, discusses
contrasting “vibration recipes” (tonal spectra) that result
from different lengths of phase 2, relative to the overall cycle length.
The specific implications of this topic for reed design are an important
subject for future reed research.
15. “Rounding of reed edges
in double-reed instruments and of edges of narrow tube entrances has been
found to influence playing: such smoothing reduces the contraction of
the free jet and consequently the turbulent dissipation losses.”
Nederveen, Acoustical Aspects, 120. By “rounding of edges,”
Nederveen was apparently referring to streamlining the outer surfaces
of the tip aperture. The reed maker or player commonly does this with
a knife, file, or fine sandpaper.
16. See Casadonte, “The Clarinet
Reed,” 350-59, for a technical discussion of this topic.
17. Smith argued that the bassoonist
must become especially adept at damping techniques in order to produce
a range of three-and-a-half octaves using a single tone generator. Smith,
Reed Design, 45.