The Not-Quite-Harmonic Overblowing of the Bassoon
By James B. Kopp
James Kopp & Associates
- The full system: bassoon, reed, and player
- What resonances are available?
- The bassoon’s in-tune second mode: how can this be?
- The first and second modes of response
- Effects of the stretched resonance curve: Third and higher modes of the bassoon
- Modal analysis of selected fingerings for modern bassoon
- End Notes
The fingering patterns of the bassoon’s upper register are based on a characteristic of its bore called the pipe resonances. Acoustic physicists have studied the pipe resonances of the Heckel- or German-system bassoon in combination with the bocal, which is in fact the upper part of the bore. In these investigations, the other components of the full acoustical system of the bassoon – the reed and the player – are purposely ignored for study purposes.1 (We will compare the full-system resonances later in this article, however.) The pipe resonances of the bassoon (hereafter understood to include the bocal) are important to the performing bassoonist as the root cause of the seemingly arbitrary fingerings in the upper register (that is, Eb4 and higher, plus a few alternate fingerings at lower pitches). (See fig.1 for an explanation of pitch names.)

Figure 1. Explanation of pitch names, based on terminology of the Acoustical Society of America.
A pipe open at one end will resonate when blown. If, for example, we blow across the open end of an empty soda bottle, a fundamental pitch is produced. An increase in blowing pressure will result in a higher “overblown” pitch. These are the pipe resonances of the bottle cavity. If the bottle’s resonant cavity is gradually reduced in size by partly filling it with water, the pitch will rise.2 This reduction is analogous to shortening the bassoon’s air column (pipe) by opening tone holes to raise the pitch from Bb1 to F3 (open F).
A pipe in the shape of a perfect cone will overblow harmonically – it will produce an array of pipe resonances related to one another by a harmonic ratio. That is, the higher resonance peaks (overtones) will be related to the lowest peak (the fundamental) by whole-number ratios of frequency. Thus the second peak (double the first peak’s frequency) will lie a perfect octave above the first, the third peak (triple the first peak’s frequency) will lie a perfect twelfth above the first, etc.3 This, roughly speaking, is how F#3 and higher pitches are produced on the bassoon.
So far, so good, but the complications start now. The bassoon’s bore is an imperfect cone in two respects. First, the cone is truncated (shortened) at the small end, the reed substituting for the missing portion. Second, there are many local perturbances (changes of slope) in the cone purposely introduced by bassoon makers, the results of experiments to improve the tuning and tone quality of the instrument.4 As a result of these two sorts of imperfections, the pipe resonances of the bassoon bore do not lie in a true harmonic relationship. Instead, the ratio is slightly stretched, meaning that the ratio of each successive higher peak increases by more than 1.0. Backus found that pipe resonances for C3 and C4 on the bassoon, for example, lay in a ratio of 1: 2.07 rather than a true harmonic ratio of 1: 2.00.5
This stretching affects the intervals at which a bassoon fingering (in other words, a pipe segment) can – after certain modifications – be made to overblow. These overblown pitches, based on overtones (upper resonances) of certain fingerings, are called the higher modal responses (or simply the higher modes) of the bassoon. Fig. 2 shows the modal responses most commonly used to produce the bassoon’s range.

Figure 2. Pipe-resonance modes commonly used for standard bassoon fingerings.
Sometimes a given pitch of the bassoon can be obtained by use of either of two modes (requiring two different fingerings, of course). The standard fingering of C#4, for example, is a second-mode response, while the long fingering for the same pitch is a third-mode response. The higher a given pitch, the greater the chance that it can be produced in more than one mode. In this sense, mode is not quite synonymous with “register.”
Certain first-mode fingerings – F2 through D3 – are the bases or ancestors, as Benade called them, of common higher-mode fingerings.6 The third, fourth, and fifth modes of these ancestors are increasingly stretched in frequency. The third mode (normally employed for Eb4 to A4) response is roughly one semitone sharp of a harmonic ratio. The fourth mode (normally employed for Bb4 through Eb5) response is one to two semitones sharp of a harmonic ratio. The fifth mode, employed for so-called “harmonic” E5 (fingered without use of a high E key) and above is, ironically, still further sharp of a harmonic ratio. (We will postpone detailed discussion of higher-mode fingerings to the appendix of this article. The reader with little appetite for the underlying theory of these fingerings may wish to skip ahead.)
One curiosity of the bassoon’s fingering technique is that the second
mode pitches (normally used for F#3 through D4) sound essentially in tune, despite
the stretched ratios of the pipe resonances. This welcome exception to the stretching
rule allows second-mode fingerings on the bassoon to be closely parallel to
their first-mode ancestors. Possible explanations for the exception are offered
below.
[Top]
1. The full system: bassoon,
reed, and player
Pipe resonances leave their imprint on the bassoon’s performance technique
(in the derivations of upper-mode fingerings), while the reed and the player,
when added to complete the system, give rise to other important acoustical characteristics.
At this point in our discussion, words can become treacherous. For clarity,
we will begin to speak of both (1) pipe resonances and (2) full-system resonances,
which include the contributions of the reed and the player’s vocal tract.
Full-system resonances are the musical sounds that bassoonists produce and listeners
experience.
The audible spectrum of any full-system resonance of the bassoon is harmonic in character; its overtones will have whole-number ratios to the fundamental.7 This remains true even if the fundamental is itself a non-harmonic upper mode of a given pipe resonance (and fingering). A concrete example will help to clarify this cumbersome statement of an important fact. The full-system spectrum of Eb4 will include, besides the fundamental Eb4 (311 Hz), higher resonance peaks (overtones) at Eb5 (2 x 311 = 622 Hz), Bb5 (3 x 311 = 932 Hz), Eb6 (4 x 311 = 1,244 Hz), G6 (5 x 311 = 1,568 Hz), Bb6 (6 x 311 = 1,864 Hz), etc.8 It is a separate issue that the fundamental (Eb4) originates as a third-mode pipe resonance of G2 (98 Hz). The frequency ratio of Eb4 to G2 is 311:98, or 3.17, a semitone above the true harmonic ratio of 3.00.9 Thus it sounds as an augmented (stretched) twelfth above G2, not a perfect (harmonic) twelfth.
Let’s talk for a moment about tone quality (timbre). If a player attempts to sound the same pitch at the same volume on the same bassoon using (a) a “bright” reed, and then using (b) a “dark” reed, the resulting timbre will differ. The difference heard by the listener will be due to the varied strengths of the respective full-system resonance peaks (fundamental and overtones) between one reed and the other. In other words, the amplitudes (strengths) of the respective resonance peaks will vary between two reeds, even though their frequencies remain unchanged. (This assumes that the two reeds play in tune with one another). Likewise, if two players – an expert (c) and then a beginner (d), let us say – sound the same pitch at the same volume on the same instrument and reed, the audible results will again differ. The amplitudes of the resonance peaks will of course differ, but this time the differences will stem from the players’ differently shaped vocal tracts (we include under this term the entire embouchure and breathing mechanism). Finally, we can obtain a slight contrast in timbre by having one player repeat the exercise using the same reed, but two different bassoons (e and f).
We can draw a useful conclusion from this exercise: variations in strengths
of resonance peaks (differences in timbre) can arise from qualities of the reed
(a versus b), from qualities of the player’s vocal tract (c
versus d), or from qualities of the pipe itself (e versus f).
Now we are in a position to examine a second influence of the pipe’s resonances
on the full-system resonances the player obtains.
[Top]
2. What resonances are available?
Fig. 3a shows the pipe resonances for Bb1. The numerals and markers below the
horizontal line are located at intervals of true harmonic ratios. The markers
above the line are, in contrast, aligned with the pipe-resonance peaks. We can
see that the pipe-resonance peaks do not align well with the harmonic ratio
markers. The higher pipe resonances of the bassoon grow increasingly sharp,
to an extent that that the eleventh pipe-resonance peak (non-harmonic) essentially
coincides with the twelfth full-system resonance peak (harmonic).10
The acoustical result of this coincidence is that the eleventh pipe-resonance
peak reinforces the twelfth full-system resonance, while the second through
tenth pipe resonance peaks offer less, or little, or even no reinforcement to
other full-system resonances.
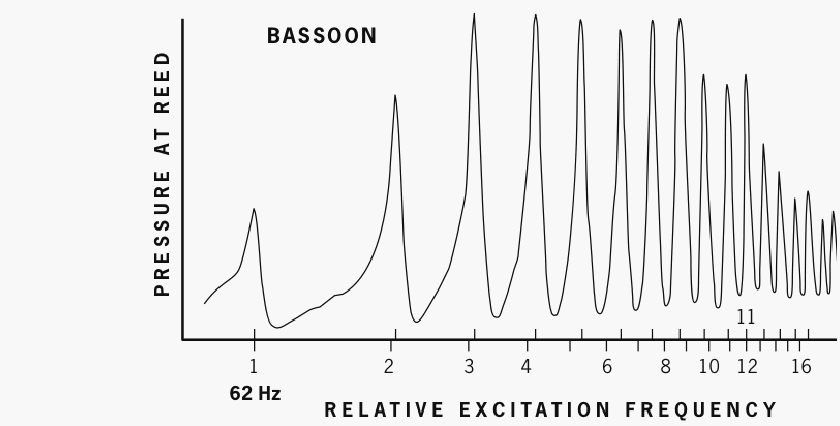
Figure 3a. Pipe resonance peaks for Bb1, lowest note of the bassoon. (Experimental conditions cause the fundamental to register sharp of the sounding pitch of 58 Hz.) Markers for the peak frequencies (atop the legend line) are increasingly sharp to the harmonic ratios (spaced below the legend line, with numbers). In fact, the eleventh resonance peak coincides with the harmonic ratio of twelve. After Backus 1977.
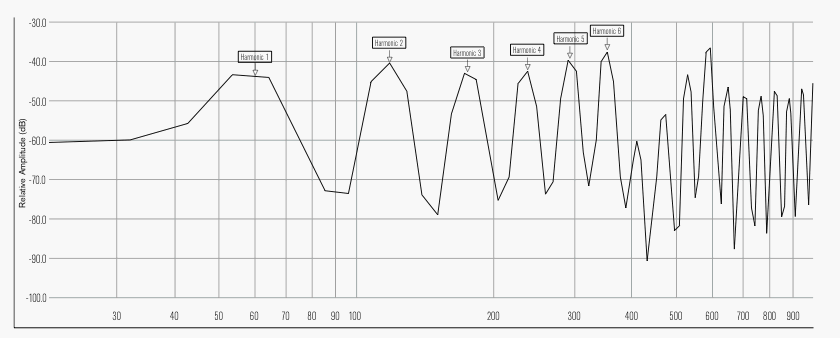
Figure 3b. Full-system resonance peaks for Bb1, the lowest note of the bassoon. When the reed and player are added to the system, peaks are located at true harmonic intervals. Graph by Leslie Ross.
As fig. 3a shows, the seventh harmonic of Bb1 is most poorly aligned with any pipe-resonance peak, followed by the sixth and eighth harmonics, followed by the fifth and ninth harmonics. The fourth and tenth harmonics show partial alignment with certain pipe-resonance peaks, while the second, third, and eleventh show substantial alignment. This extensive alignment of resonance peaks with harmonic ratios at relatively low frequencies is why Bb1 is noticeably rich in overtones.
But such is not always the case. Backus gave striking examples of how little the pipe sometimes contributes to the full-system resonance of some tones:
For the note F3, just before the break [open F, highest note of the first mode], there is only one strong resonance, giving the fundamental; the resonance curve for this note is shown in Fig. [4a]. As can be seen from this curve all of the higher resonances are small, and their frequencies do not coincide with the harmonic frequencies [that is, the resonance frequencies are sharp]....
(See fig. 4a.) This is the main reason why open F sounds thin in timbre, compared to some lower notes.
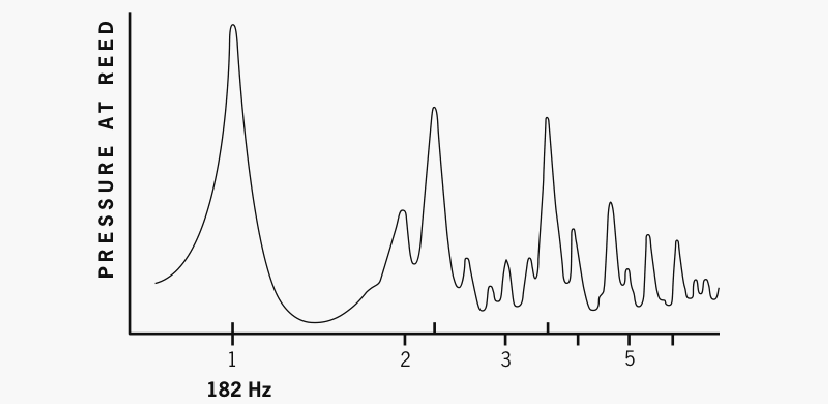
Figure 4a. Pipe resonance peaks for F3 (open F). (Experimental conditions cause the fundamental to register slightly sharp of the sounding pitch of 175 Hz.) Only one strong resonance peak, the fundamental, coincides with a harmonic ratio. After Backus 1977.
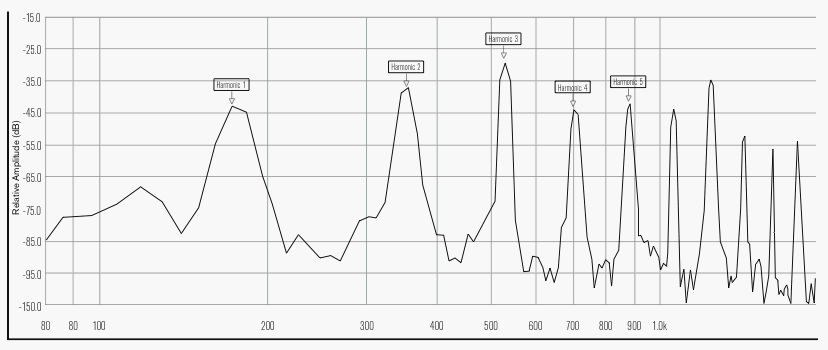
Figure 4b. Full-system resonance peaks for F3. When the reed and player are added to the system, peaks are located at true harmonic intervals. Graph by Leslie Ross.
Backus continued:
The second resonance is used for the notes up through D 4. The next note Eb4 is obtained by cross fingering; the vent hole thus provided reduces the heights of the first two resonances and encourages the instrument to vibrate on the third resonance [of the pipe] .... [See fig. 5a.] There are no resonances so placed as to reinforce the higher harmonics. This is typical of the highest notes on the instrument; if a resonance coincides with a harmonic above the fundamental, it does so only by chance.11
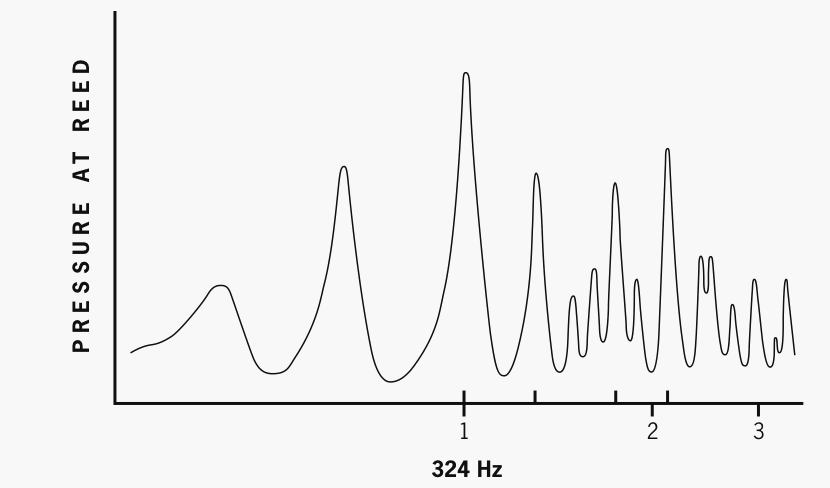
Figure 5a. The third peak from the left, marked 1, is the pipe resonance
that the bassoon bore contributes to the sounding pitch Eb4. (Experimental conditions
cause the fundamental to register sharp of the sounding pitch of 311 Hz.) No
strong pipe resonances align with the harmonic ratios of Eb4 (marked as 2 and
3). After Backus 1977.
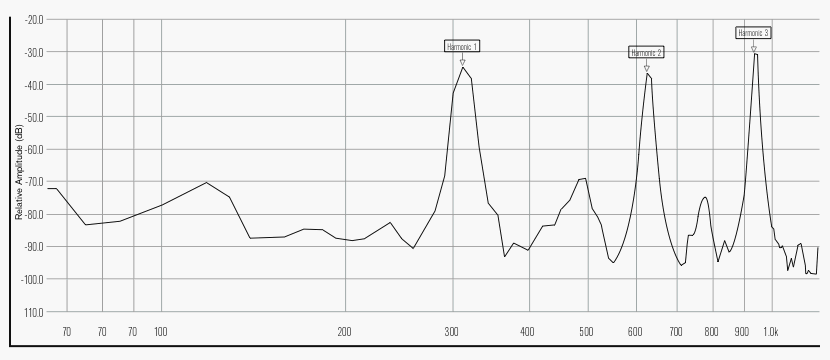
Figure 5b. Full-system resonance peaks for Eb4. When the reed and player are added to the system, peaks are located at true harmonic intervals. Graph by Leslie Ross.
We may pursue Backus’s thought a little further to a useful conclusion.
The bassoon is played using its first five modes. Within these bounds, we may
say that the higher the mode number, the weaker the reinforcement of lower harmonics
by the pipe resonances will be. (Recall the progressively greater misalignment
of lower harmonics with the pipe-resonance peaks of Bb1.) In this sense, the
stretching of the pipe-resonance frequency ratio is directly responsible for
the thinner timbre in the bassoon’s upper modes.
Now let’s compare the corresponding graphs of full-system resonances. (See figs. 3b, 4b, 5b.) For each of the three notes graphed by Backus, we now see an array of many strong resonances, each peak lying at a predictable, harmonic ratio from the fundamental. If not from the pipe, where do these second and higher peaks come from? The answer is, they come from the other components of the bassoon’s acoustic system – the reed and the player. Both the reed and the player’s vocal tract have a wide range of resonances available to contribute to the system. For any sounding pitch, some of these resonances enter into systematic collaboration with the pipe to produce a musical tone, and the result is what acoustic physicists call a regime of oscillation.
The regime is less tidy than the picture sometimes painted for pedagogical purposes. It resembles to some extent an invisible game of musical chairs, in particular one where the rules have been altered. In this altered game, which we might call “harmonic chairs,” the chairs are arranged in a pattern of harmonic relationships, although the absolute pitch levels are not predetermined. After a fingering is chosen and the music starts (remember, the rules have been altered), all available resonances scramble to find chairs. The strongest and most harmonically attractive resonances that are available grab seats in a few milliseconds, and the absolute pitches settle at whatever is the most stable regime of oscillation. (It’s helpful to note that resonance peaks often have broad bases covering a range of frequencies on either side of the peak itself, as shown in figures 4b and 5b. Thus there is often some negotiability in setting up the regime of oscillation. But the further off-peak, the weaker the resulting harmonic will be.)
This does not necessarily mean that the lowest resonance gets the most comfortable chair; it may be forced into a chair that’s a little sharper or flatter than it would prefer. If the lowest available resonance is harmonically unrelated, it will get no chair at all. In other words, it (like other available resonances) may not participate in a particular regime of oscillation. But once the player changes to a different fingering, it’s time for a new regime of oscillation and a new game of harmonic chairs.12
As a participant in these regimes, a superior instrument, reed, or player will
make its/his/her excellence felt. Totally aside from the stretched ratio we
discussed above, the further alignment of pipe resonances in individual bassoons
can range from excellent to poor, giving rise to a corresponding range of tonal
beauty, or lack thereof. The “best” bassoon for a player will be
the one that, through well-aligned resonances and maximum flexibility, makes
the largest contributions to the hundreds or thousands of different regimes
that must arise during the performance of a musical work. Much the same is true
for the “best” reed, which has to contribute a range of appropriate
resonances even while its shape and size are changed by vibrations and by the
player’s embouchure. Different players will contribute different resonances
according to the differing shapes of their vocal tracts. But this is neither
the only edge the superior player can have, nor the most important one. Audibly
superior tone results when a player is able – consciously or unconsciously
– to adjust his/her embouchure for stronger resonance, and for a broader
range of resonant frequencies, the better to accommodate the exact pitch required
by an ensemble at a given moment. The superior player can optimize resonance
at extreme dynamic levels, at quick speeds of execution and, at times, while
in the throes of muscle fatigue. A “great sound” on the bassoon
is always achieved through a strong regime of oscillation.
[Top]
3. The bassoon’s in-tune
second mode: how can this be?
We noted earlier that the bassoon’s full-system, second-mode response
is essentially in tune – it overblows at a harmonic ratio of 2:1. How
does this happen, given that the pipe resonances are stretched? Part of the
answer lies in the small degree of stretching that would be expected in the
second mode. Given that the bassoon’s third- mode response is one semitone
sharp of harmonic, we might suppose that the second-mode stretching would be
less. Backus’s findings support this guess.13
A second part of the answer may result from a trait of any woodwind’s acoustical system called the cutoff frequency. The cutoff is a frequency above which all the tone holes left open in a given fingering begin to participate in the standing wave (the basic musical vibration of the bassoon or other woodwind). This sounds at first like a rather remote concern to the performing bassoonist, but such is not the case. What’s significant is that the full-system resonances are boosted in strength – but lowered in frequency – in the proportion by which they exceed cutoff frequency. This is because higher-frequency vibrations, being increasingly shorter in wavelength, are more and more able to reach into the open tone holes. Thus the open tone holes increasingly become part of the vibrating air column.
Experts sometimes describe the bassoon’s cutoff frequency as a range, and other times as a single frequency. It has been reported as broadly as “300 Hz to 600 Hz” (that is about D4 to D5) or as narrowly as “about 400 Hz” (a little above G4 = 392 Hz).14 Under any of these interpretations, however, the general effects are not in question. In the following discussion, we will assume that cutoff frequency is around 400 Hz.
The higher the vibration frequency lies above cutoff, the more completely the “tails” of the air column reach into the open tone holes. As they do so, the volume of the tone holes is added to the main bore volume, and the bore is effectively enlarged. This enlargement results, as might be expected, in a flattening of the higher overtones, as compared to the fundamental. The spectrum of the full-system peaks is therefore described as compressed. This compression of the resonance frequencies above cutoff can flatten an entire regime of oscillation.15
With these unquestioned aspects of the bassoon’s acoustical behavior in mind, we can now put forth an educated guess about the intonation of the bassoon’s second mode. It may not be mere coincidence that virtually all the overtones of the bassoon’s second- and higher-mode tones lie above cutoff (whereas Bb1, in contrast, has five overtones below cutoff). The frequency compression of the full system’s overtones above cutoff may help to balance the stretching of the pipe resonances, as the sharp fundamentals of the second-mode pipe resonances are lowered in regimes of oscillation dominated by flattened overtones. In time, acoustics researchers may devise experiments to test this hypothesis.
We’ve been speaking of the bassoon’s second mode as if it were
perfectly in tune. For some fortunate players and/or instruments, this is true.
It is not uncommon, however, for the exact pitch and/or resonance of the notes
A3, Bb3, B3, C4 and D4 to require tweaking through bocal choice, reed design,
or the player’s embouchure.16
Some players resort to more elaborate fingerings, such as holding open a secondary
speaker (“flick”) key, etc. Meanwhile, C#4 is also flat on some
bassoons. A common remedy is the use of well-known “long” or “full”
fingerings, which raise the pitch (by a shift into third mode). This well-known
range of remedies suggests that a precisely harmonic second mode is not a given,
even when the corresponding first-mode pitches are well in tune. The problem
may result from imprecise bore perturbations (sometimes including a poorly chosen
bocal), from more-than-optimal compression of overtones above cutoff (as described
above) in some individual bassoons, or from still other factors.17
[Top]
APPENDIX: MODE AND ANCESTRY IN BASSOON FINGERINGS
4. The first and second modes
of response
The lowest 19 semitones of the bassoon’s scale (Bb1 through F3) are obtained
as fundamentals of a gradually shortened pipe. (We are speaking here of the
modern Heckel or German system, including whisper key.) The higher pitches are
obtained by overblowing – by inhibiting production of the pipe’s
lower resonance(s), so that a higher resonance is heard as the sounding pitch.
This is accomplished by altering the frequency of the first- mode peak so that
it no longer fits into the harmonic regime of oscillation.18
As bassoonists know, the second mode (or register) is produced
as octaves of the first mode. Benade referred to such first-mode fingerings,
the bases of higher-mode fingerings, as ancestors.19
Small differences separate second-mode fingerings from their ancestors. To produce F#3, we partially open the first finger hole. This makes the upper octave speak securely, but it also has a side effect: it slightly sharpens the pitch. A brief experiment will clarify this: attack and sustain F#3 while gradually closing the half hole. Its volume will diminish, and the pitch will sag. If we repeat the experiment with a simple fingering for G3 (/xx xxx), we get a similar result. But if we then add the Eb key (a common remedy for a sharp G3), we find that the size of the “half-hole” opening matters little.20
The register-key vent, in contrast to use of a half-hole, does not cause appreciable sharpening. Backus’s explanation for the clarinet’s register-key vent is also valid for the bassoon’s whisper-key vent:
This hole essentially destroys the lowest resonance.... The lowest resonance moves from its position as shown by the solid line ... to that shown by the dotted line when the vent-hole is opened; the remaining higher resonances are essentially unchanged.)21 [See fig. 6.]
After the frequency of the lowest resonance has been shifted, the lowest resonance is unable to participate in the regime of oscillation. The regime is instead based on the next-higher mode, the bassoon’s second or the clarinet’s third.
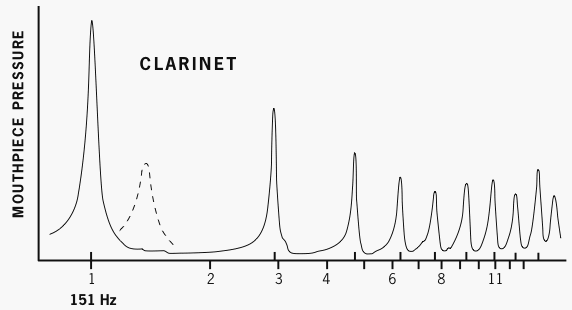
Figure 6. Effect of the register key. The dotted line shows the shifted frequency of the lowest resonance after the vent-hole has been opened. This graph, after Backus 1977, is for clarinet, but the effect of the bassoon’s whisper key is comparable.
5. Effects of the stretched resonance
curve: Third and higher modes of the bassoon
It’s not hard to recognize relationships between second-mode fingerings
of the bassoon and their first-mode ancestors. Bassoonists who double on clarinet
have no doubt grasped the ancestral relationship between some of the clarinet’s
third-mode fingerings (written B4 to C5) and their first-mode ancestors (written
E3 to G2). But fingerings for the bassoon’s third mode (Eb4 through A4)
are less obviously related to their ancestors.22
The root cause of the obscurity is the stretched resonance curve of the bassoon’s
pipe resonances, as discussed above. Because of this stretching, standard bassoon
fingerings have to be based on an odd-looking but right-sounding interval. Even
under this “offset” scheme, ancestral relationships are further
obscured, at first glance, by the opening of various tone holes as cross-finger
vents. At second glance, however, the siting of these cross-finger vents in
fact follows roughly predictable patterns. Each new cross-finger vent in the
table is incrementally higher, tracing in miniature the rise of the sounding
pitches. After a simple pattern in mode 2, a new pattern is initiated in modes
3 and 4. (See fig. 7.)


Figure 7. Pattern of cross-finger vents on bassoon. Both the fingerings and their representation are based on the Bassoon- Family Fingering Companion by Terry B. Ewell and Lisa Hoyt, online at http://www.idrs.org/bsnfing/fingnote.htm.
The opening of cross-finger vents often has the additional effect of further sharpening an already sharper- than-harmonic, third- or fourth-mode resonance. The resulting sharpness is sometimes negligible, but at other times it is a matter of a semitone. For fine-tuning of these and other intonation problems, tone holes (often much further down the bore) are closed or opened. Still other tone holes may be closed to enhance resonance. Examples include the addition of the F key to the pitch G3 and the addition of the Eb key to the pitches E4 through A4. These fingering needs make ancestral relationships still harder to discern. (See fig. 8.)

6. Modal analysis of selected
fingerings for modern bassoon
Third-mode response of the bassoon is one semitone sharp of a harmonic ratio,
after sharpness due to cross-finger venting is included. Eb3 marks the lowest
standard fingering of the third mode, but some lower alternate fingerings from
the mode are frequently employed, including the long C4.23
Ancestor fingerings from F2 to C3 produce C4 through A4. (See fig. 9.)

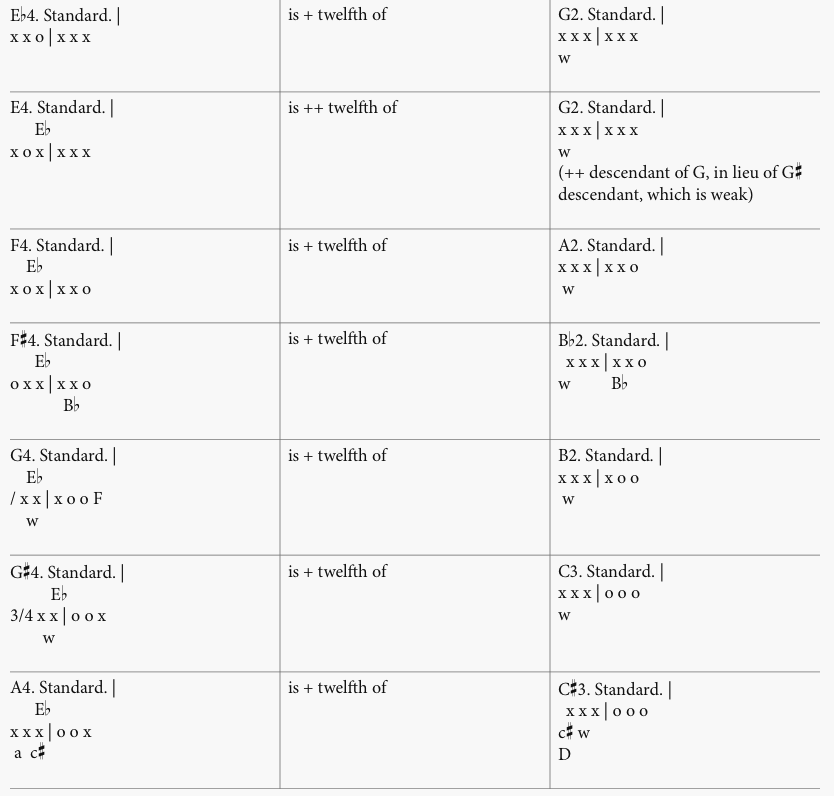
Figure 9. Ancestors of third-mode fingerings. The left column shows selected standard third-mode fingerings; the right column shows the relevant first-mode ancestor fingerings. “+ twelfth” denotes the interval of an augmented twelfth; “++ twelfth” denotes the interval of a double-augmented twelfth. Fingerings based on Ewell and Hoyt.
Fourth mode is based on a narrower range of ancestors – from A2 to C#3. B4 and B4 are one semitone sharp of a harmonic ratio, while C5 and higher are two semitones sharp. (Again, part of this sharpness is due to the sharpening effects of some cross-finger vents.) (See fig. 10.) The fourth mode traditionally extends through “harmonic” D#5. However, certain left-hand keys, if present, may be used to obtain a different D#5, and even E5 and F5, all of these being sharpened versions of the D5 fingering. Fingered thus, all of these are in fourth mode.


Figure 10. Ancestors of fourth-mode fingerings. The left column shows selected standard fourth-mode fingerings; the right column shows the relevant first-mode ancestor fingerings. “+ twelfth” denotes the interval of an augmented twelfth; “++ twelfth” denotes the interval of a double-augmented twelfth. Fingerings based on Ewell and Hoyt.
The bassoon’s fifth mode begins at “harmonic” E5, using fingerings that may be consulted on the web site http://www.idrs.org/bsnfing/fingnote.htm. The numerous available fingerings for the fifth mode are more difficult to analyze with certainty, due to increasing complications and the increasing sharpness of the ancestral resonance peaks. For example, is E5 the quadruple-augmented seventeenth of G2, as one fingering would imply? Or is it the triple-augmented seventeenth of G2, as another fingering would imply? (See fig. 11.)

Figure 11. Two fifth-mode fingerings for E5. These two sample fingerings show that a single pitch can have fingerings based on different ancestors, even within the same mode. Fingerings based on Ewell.
At the borders between modes, a relatively open lower-mode fingering will be neighbor to a relatively closed higher-mode fingering. During an ascending slur to the higher mode, a mildly percussive white noise is an audible clue that mode shifting is at work. This rough transition makes for some crunchy trills between such neighbors as F3/F#3, D4/Eb4, A4/ Bb4, and “harmonic” D#5/E5.
Mode shifts also make for treacherous longer slurs, especially slurs downward to a lower mode. A bassoon passage in the Tchaikovsky Fifth Symphony, third movement, provides a well-known example. (See fig. 12.) Four downward slurs between third- and second-mode pitches precede a second- to first-mode slur. In the absence of a tongued articulation, the player often uses a speaker key to assure the mode shift. The player may also use the embouchure, wind velocity, and well-designed, flexible reeds to help minimize this difficulty.

Figure 12. Slurs between modes. The numerals in the fourth through seventh measures indicate the modes of the respective fingerings. This excerpt is from Tchaikovsky, Symphony 5, third movement.
The structural sharpness of higher-mode responses of the bassoon is seldom questioned by its long-suffering players, who patiently learn the bizarre-looking fingerings by rote. It may provide some practical guidance, however, and it certainly provides some moral support, to know that there is a method to the seeming madness of these fingerings.
REFERENCES
Backus 1974. John Backus, “Input Impedance Curves for the Reed Woodwind
Instruments.” Journal of the Acoustical Society of America 56/4
(October), 1266-79.
Backus 1977. John Backus, The Acoustical Foundations of Music, second. ed. New York: Norton.
Baines 1991. Anthony Baines, Woodwind Instruments and their History, third ed. New York: Dover.
Benade 1960. Arthur H. Benade, Horns, Strings & Harmony. Garden City, New York: Anchor Books (Doubleday).
Benade 1990. Arthur H. Benade, Fundamentals of Musical Acoustics, second, rev. ed. New York: Dover.
Corey 1980. Gerald E. Corey, “How to Improve your Tuning on the Bassoon,” Journal of the International Double Reed Society 8, 28-34.
Cronin 1996. Robert H. Cronin, “Understanding the Operation of Auxiliary Fingerings on the Modern Bassoon,” Journal of the International Double Reed Society 24, 23-30.
Fletcher and Rossing 1991. Neville H. Fletcher and Thomas D. Rossing, The Physics of Musical Instruments. New York: Springer.
Nederveen 1998. C. J. Nederveen, Acoustical Aspects of Woodwind Instruments, revised ed. DeKalb, Illinois: Northern Illinois University Press.
ACKOWLEDGEMENTS
I would like to thank Frank A. Morelli and C. J. Nederveen,
who read this article in draft and made numerous useful suggestions. I would
also like to thank Leslie Ross, who recorded my bassoon playing
and prepared the graphs of full-system responses.
New material copyright 2006 by James B. Kopp
James B. Kopp has been a commercial reed maker (and teacher
of reed making and adjustment techniques) since 1991, specializing in reeds
for bassoon, contrabassoon, and early bassoon.
7. End Notes
1 In the researchers’ “external
excitation” method, the bassoon is “fingered” by the use of
stoppers and wedges to close the appropriate holes and keys, while an external
sound source – in effect, a tiny speaker with carefully controlled volume
– is used to excite the pipe resonances. Using a small microphone, the
researchers measure the results in acoustic ohms. See Backus 1974: 1273-79 for
a detailed description.
2 Benade 1960: 148-49. When Benade described this experiment, six-ounce Coca-Cola bottles were common. Today’s broad-shouldered bottles do not overblow as readily. The experiment can be performed more easily using a long, narrow vessel like a test tube.
3 I have simplified the issues here for purposes of discussion. In reality, a phenomenon called frequency- dependent wall damping causes slight shifts in the resonances, as C. J. Nederveen pointed out to me. Even truly harmonic overtones, if the bassoon produced them, would result in just intonation, not the equally tempered scale to which modern pianos are tuned.
4 “... the different sections in the bassoon ... have conical bores of different tapers. Furthermore, the cone is not complete out to the tip, but is cut off short of the tip and the reed substituted; the bassoon would be some 30 centimeters (12 inches) longer if it were a complete cone. These factors produce deviations of the resonance frequencies from the desired tempered scale values....” Backus 1977: 238.
6 Benade 1960: 224. The bassoon has an unusually large downward extension of range. But pitches below F (sometimes called the seven-finger pitch, to simplify comparisons to other woodwinds) are not normally used as the basis of higher modes. Meanwhile, the highest first-mode fingerings – Eb3 through F3 – serve as ancestors only for “technical” alternate fingerings.
7 This is true during sustained tones, but not during attacks.
8 Rounding prevents some of these products from matching exactly.
9 A portion of this increase in ratio is due to the additional sharpening effect of the cross-finger vent; this effect is discussed below.
10 Backus seems not to have addressed the pitch-ratio discrepancy between pipe resonances and full-system resonances in print, although he would surely have been aware of it. The following statement neglects the issue: “The actual playing frequencies of a reed instrument are therefore approximately the same as the resonance frequencies measured for the air column with the reed end closed [the pipe, that is], and thus correspond to the high impedance peaks for the input impedance curves. The intonation of a given instrument will then depend critically on the frequencies of the impedance peaks.” Backus 1974: 1266.
12 This interaction is explained more technically in a theory called interlocking or mode locking. See Benade 1990: 445; Fletcher and Rossing 1991: 143-44. Multiphonic tones are an exception to this scheme; see Backus 1977: 250-51 and Benade 1990: 565-55, for an introduction.
14 “[Benade’s] measurements show that musically satisfactory instruments have cutoff frequencies within the range ... 300-600 Hz for bassoons.” Fletcher and Rossing 1991: 476. This statement seems to be a liberal interpretation of Benade 1990: 487-88, fig. 22.8, where a graph shows cutoff frequencies for baroque, Buffet, and Heckel-type bassoons. The range shown for Heckel 7170, most appropriate to our discussion, appears to extend from about 380 Hz to 520 Hz. Meanwhile, Cronin 1996: 24 found that “The bassoon’s cutoff frequency is about 400 Hz over most of the range of the instrument.”
15 Benade remarked on the potency of the overtone compression: “... an air column provided with open tone holes ‘looks’ longer when it is asked to vibrate in a high-frequency mode than it does when it is vibrating in a lower-frequency mode. On woodwinds, this phenomenon by itself accounts for a flattening of any upper resonance frequency relative to the lowest one. This flattening (which can amount to an appreciable fraction of a semitone) may need to be offset by alterations in the bore profile when the instrument is adjusted to play properly.” Benade 1991: 432-33.
16 Corey 1980: 30-32 found these pitches to be “often flat” or “almost always flat.”
17 See Nederveen 1998: 90-91 for a technical discussion of the effects of closed key holes and bore perturbations.
18 Cronin 1996: 23 described the production of the third and higher modes: “The effect [of cross-fingerings] is to misalign the lower air-column resonances while strengthening the third, fourth or fifth resonance so that a high note is produced.” He drew a distinction between cross fingerings and half-hole fingerings, writing that “small vents opened to facilitate octave overblowing are not considered tone holes in this definition.” Yet the half-hole can at times have the effect of sharpening the second-mode response, just as the cross- finger vent sharpens the higher-mode responses.
20 The particular sharpness of G3 is a complicated matter outside the scope of our discussion. See Cronin 1996: 26 for a detailed explanation.
21 Backus 1977: 228. For further comments, see Benade 1990: 455.
22 Baines wrote that “the high register of the bassoon is obtained by sharp-sounding harmonics that almost defy analysis.” These sharp resonances are not harmonics, to speak precisely, but we understand that Baines was describing the stretched resonance curve. He continued, “To give two of the less mystifying examples, A4 and E5 on the German model are made as third and fourth harmonics of low-register C#3 (theoretically G#4 and C#5 respectively).” Baines 1991: 38.
23 “The various ‘long fingerings’ for C#4 are also cross-fingerings.” Cronin 1996: 23.